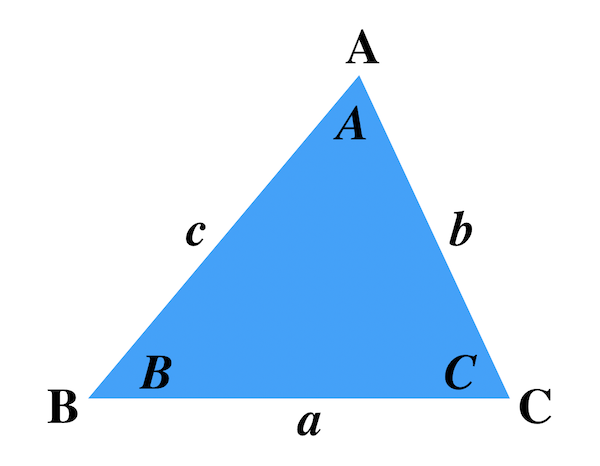
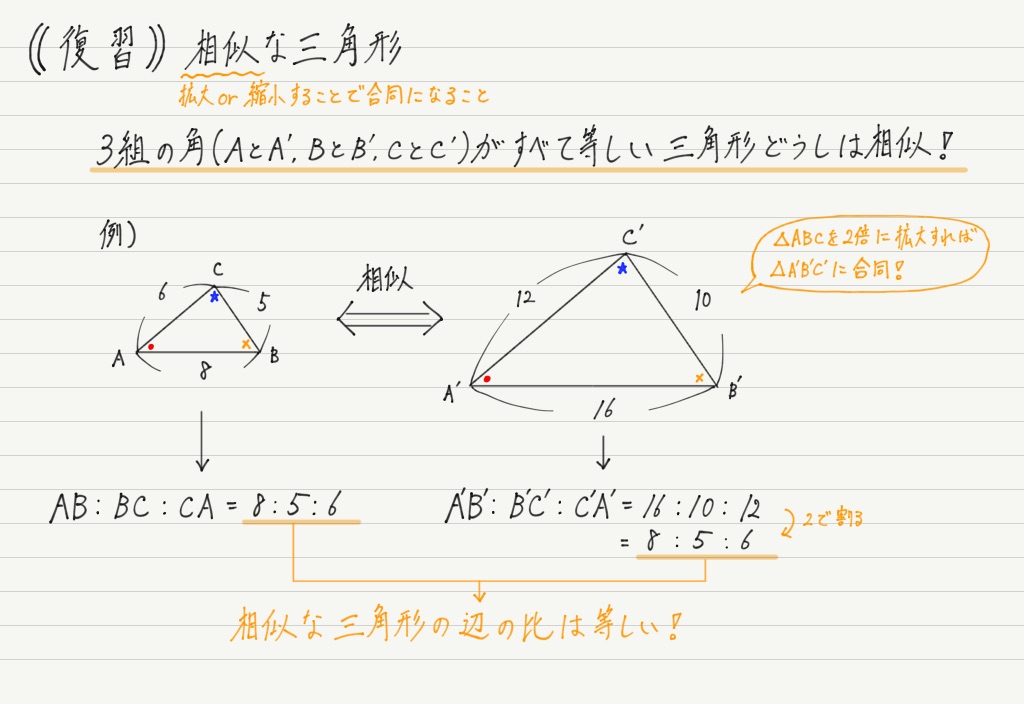
画像 三角比 長さ 求め方 174120

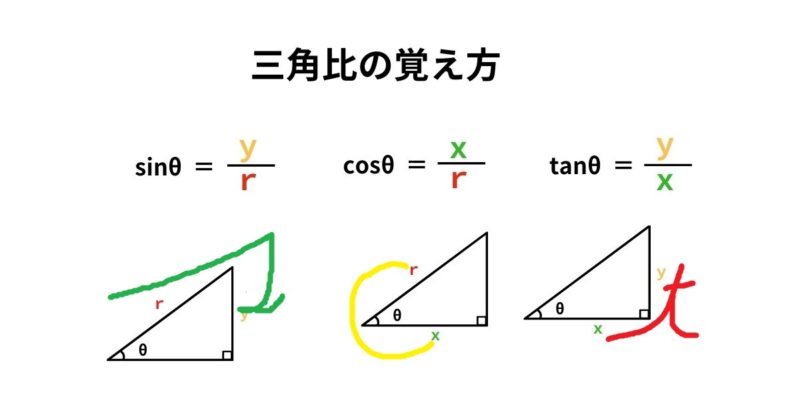
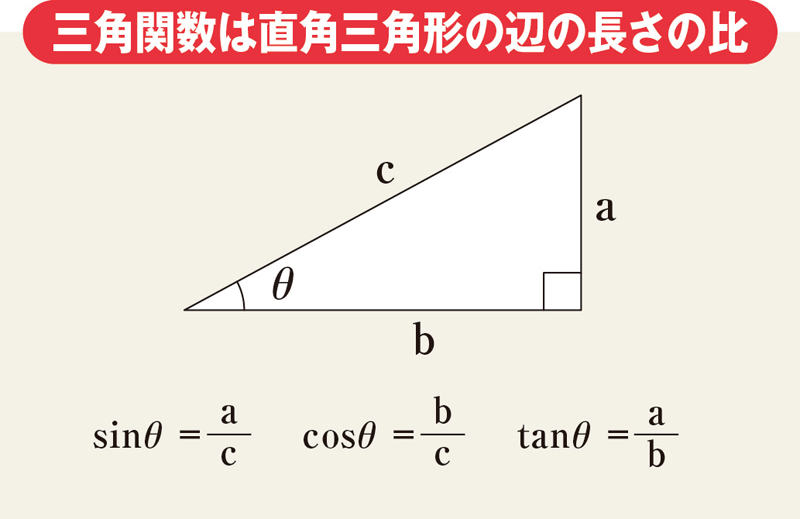
 このページは、このような人に向けた内容となっています \(\sin, \cos, \tan\)が何のことなのかイマイチ分からない \(\sin, \cos, \tan\)の求め方がわからない \(0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}, 90^{\circ}\)の三角比（\(\sin, \cos, \tan\)）が覚えられない 三角比を学ぶ上で必ずマスターしなければいけない余弦と呼ばれ（隣辺）÷（斜辺）で定義されるもの： （「コサイン・シータ イコール アール分のエックス」と読む） 正接と呼ばれ（対辺）÷（隣辺）で定義されるもの： （「タンジェント・シータ イコール エックス分のワイ」と読む） ※ 角度が決まらないと直角三角形の辺の長さの比は決まりませんので， 「サイン sin 」とか「コサイン cos 」というものはない三角比とは、 直角三角形の比 を表す値だよ。 直角三角形 って、 あるもの が決まると、 辺の長さの比 が1つに決まるんだよ。 中学校で勉強した内容だけれど、覚えているかな？ それは、 「角度」 。 直角三角形は、角度が決まると辺の長さが決まるんだ。 特に有名で重要なのは、2つの 「三角定規」 のパターンだよ。 POINT

数i 基本的な三角比の値

三角比 長さ 求め方

三角比 長さ 求め方-三角形とは？面積の公式や、角度・辺の長さ・重心の求め方 Excel三平方の定理で直角三角形の辺の長さ、面積、角度を 高校数学Ⅰ 三角比辺の長さの求め方まとめと問題 manabShopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations

三角関数について

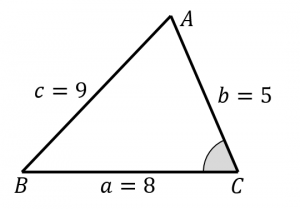
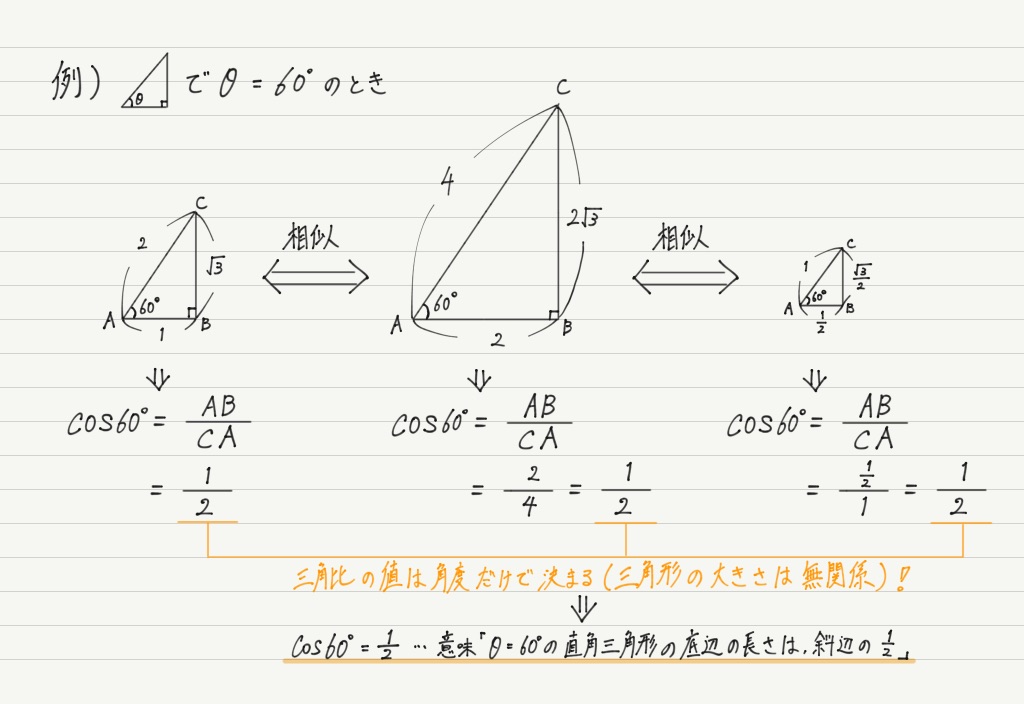
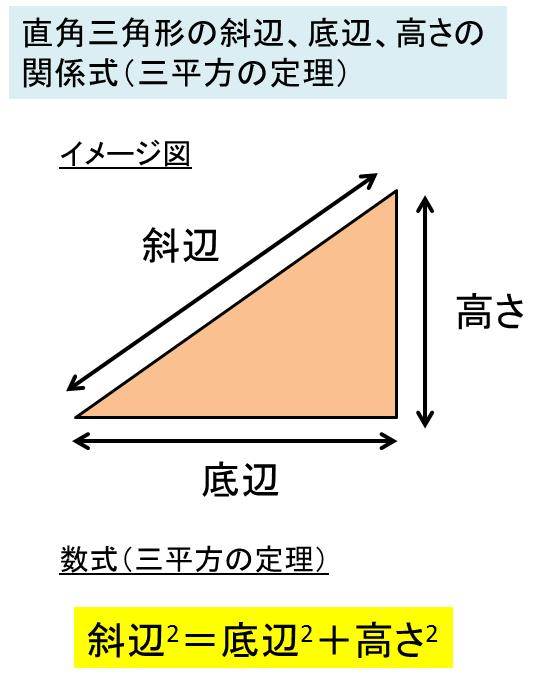
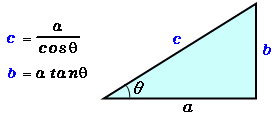
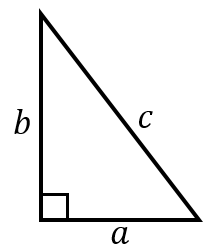
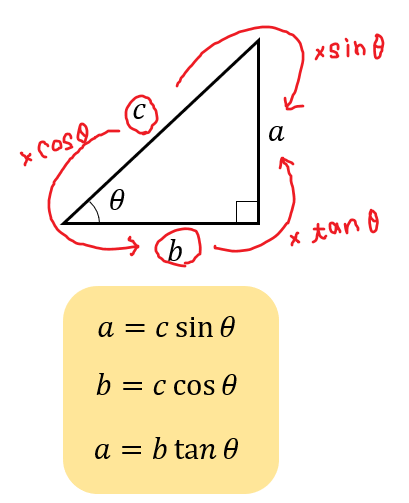
直角三角形の各辺の長と三角比の関係 直角三角形の1辺の長さと，直角でない1つの内角がわかっている場合の各辺の長さを三角比を用いて表す． AB = c とすると， sin θ = BC AB より， BC = c sin θ cos θ = AC AB より， AC = c cos θ BC = a とすると， sin θ = BC AB より つぎの直角三角形の辺の長さxを求めてください。 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角まず，30°，45°，60°の角をもつ特別な直角三角形の3辺の比を確認しておきましょう。 ですね。 上記の30°，45°，60°の三角比は，いつでも使えるようにしておくことが大切です。 ≪正弦定理を用いて三角形の辺の長さを求める≫ では， 問題 ABCにおいて， a ＝3， A ＝60°， B ＝45°のとき， b を求めよ。 を解いてみましょう。 a と A ， b と B は向かい合う辺と角だ

長さを求めよ。「三角比の表」によると、sin65 о＝ ，cos65 о＝ B 10 m 65 о A C 問8．右の三角形ABCにおいて、 B (1) cos αの値を求めよ。 cos α＝ 5 (2) 右下の「三角比の表」の一部を用いて、αの値を言え。 (整数値で答えよ。) A α三角比を求められるようにしておきましょう。 30° 45° √3 1 1つの角が 30° である直角三角形の辺の比は 1∶2∶√3 となっているので，sin30°= また，1つの角が 60° である直角三角形の辺の比も同様なの直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか？ 三角形の比についてよくわからない方は、三角比（30°,45°,60°） をみてください。 それでは、sin30°、cos30°、tan30°の求め方を説明していきます。 sin30°の求め方 上の直角三角形に描いてある水色の線を見てく

三角比は，直角三角形の辺の比を表します。 長さがわからない辺があるので，まずは三平方の定理を利用してすべての辺の長さを求めましょう。 次に，定義に従って三角比の値をそれぞれ求めます。 今回の問題では が左下にあるので簡単に求められます。三角形の辺の長さを求めるときの三角比の値 下の図の x の値を求めよ。 これを解こうとすると，sin45°，sin60°という三角比が出てきました。 定義では，「直角三角形」だけで考えるとありました。 しかし，この三角形は直角三角形ではないのに，どうしてsin45°，sin60°があるのですか。 進研ゼミからの回答！ こんにちは。 いただいた質問について，さっそく直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

タンジェントとは何か 中学生でも分かる三角関数の基礎

問2 図2の場合の三角比をX，Y で表せ。 sinθ= cosθ= tanθ= 問3 図3を見て次の問に答えよ。 (1)点Pの座標を求め，135 の三角比を求めよ。 P( , ) sin135 =cos135 = tan135 = (2)点Qの座標を求め，45 の三角比を求めよ。 Q( , ) sin45 =cos45 = tan45 =4 三角形の外接円の半径を求めてみる 41 三角形の1辺の長さとその対角がわかっていたら？ 42 対角がわかっていないなら？ 43 四角形の外接円の半径も求めることができるとなることがわかります。 次に円の中心 O から辺 BCに向かって垂線を下ろし、辺 BC との交点を点 F とします。 また OB=OC= R より、 BOC は二等辺三角形だとわかりますね。 よって \\ \begin {eqnarray} \angle BOF &=& \angle COF \\ &=& \frac {1} {2}\angle BOC \\ &=& \frac {1} {2}\times2\angle BAC \\ &=& \angle BAC ・・・ (1) \end {eqnarray} \\

正弦定理 余弦定理の求め方 三角形いろいろ 三角比の応用 エミュー

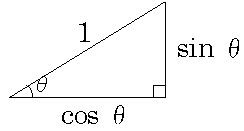
三角関数の初歩

三角 関数 長 さ の 求め 方 三角形の辺の長さを求めるときの三角比の値 下の図のxの値を求めよ。 これを解こうとすると，sin45 ，sin60 という三角比が出てきました。Sinθ＝ 対辺 ／ 3 より 対辺 ＝ 3 sinθ となります。 このとき、 対辺の長さが座標軸における点Pのy座標 となります。 cosθ＝ 底辺 ／ 3 より 底辺− 95 − 高校講座・学習メモ ベーシック数学 29 三角定規の性質 問題3 1辺の長さが1の正八角形の面積を求めなさい。 考え方 右図のように，1

底辺と高さから角度と斜辺を計算 高精度計算サイト

3

鋭角の三角比 §2 三角比 2．鋭角の三角比 ここでは，前の章で説明した三角比の定義だけでは，まだ理解できないと思いますので，いろいろな三角形を用いて三角比の定義の理解を深めていくことにしましょう。 そこで，もう一度，三角比の定義のお中学生からの質問（数学） や が出てくるのは，次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため，3つの角が30°，60°，90°である直角三角形と，45°，45°，90°である直角三角形の3辺の長さには，それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°，60°，90°の 参考リンク：三平方の定理と辺の長さの求め方！絶対にわかる証明の図解付き 正三角形の性質と辺の長さ 正三角形も広い意味で二等辺三角形と言えます。正三角形の性質と辺の長さを求める頻出の問題をみてみましょう。 性質

三角形の面積を３辺の長さから求める２つの方法 具体例で学ぶ数学

三角比の測量への利用 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信

直角三角形の底辺と高さから傾斜角と斜辺を計算します。 答えの度分秒（° ′ ″ ）は、秒の小数点以下2桁まで求めています。 \) お客様の声 アンケート投稿 よくある質問 リンク方法 底辺と高さから角度と斜辺を計算 110 /721件 表示件数 1 直角三角形の辺の比の3つのパターン 直角三角形の比は3つ覚えればいい？？ こんにちは！ぺーたーだよ。 三平方の定理で覚えておきたいのは、 直角三角形の比 だよ。 これを覚えておけば、 三平方の定理を使わなくて辺の長さを計算できちゃうんだ。If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to

三角比から辺の長さを求める 数学i フリー教材開発コミュニティ Ftext

三角比の表と面積公式 正弦定理 余弦定理を一記事で解説

鈍角の三角比の求め方 解答左の図を見ながら，順を追って説明していきましょう。 ① 半円を描き，半径 (動く半径のことを 動径 と呼びます) を 1ﾟ 動かします。

高校数 三角比 三角形の面積 直角三角形 オンライン無料塾 ターンナップ Youtube

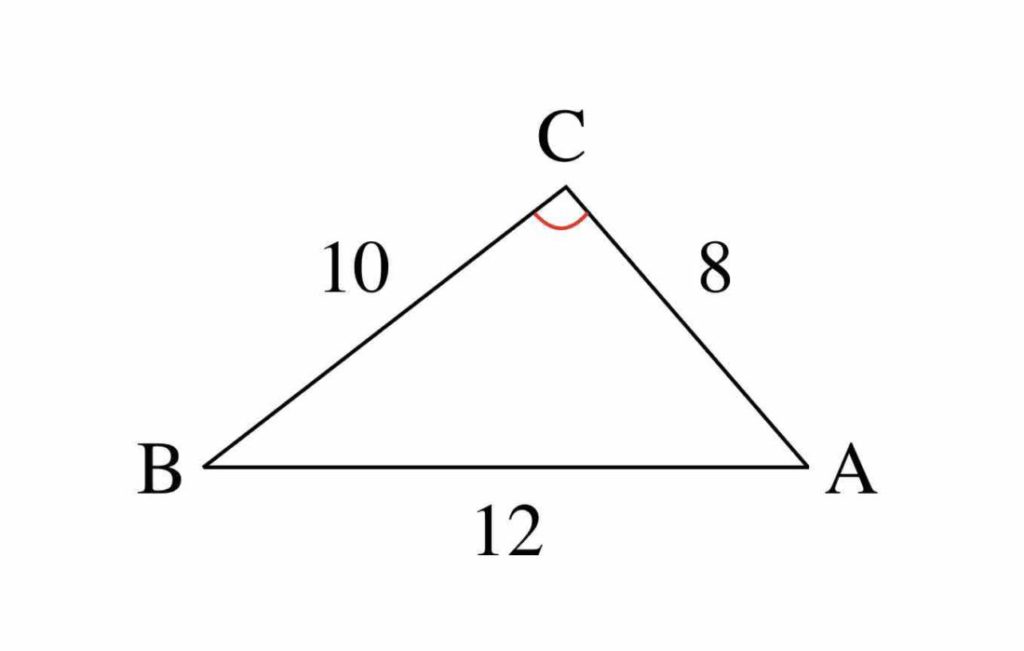
高校数学の三角比について質問です 図において Cdとbcの辺の長さ Yahoo 知恵袋

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月

三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局

三角比について

三角関数のsin Cos Tanとは 図解ですぐわかる 超重要な公式と練習問題も 高校生向け受験応援メディア 受験のミカタ

数i 基本的な三角比の値

底辺と角度から 高さを求める ある高さの木から 10m離れて 木の 数学 教えて Goo

三角比を使って円に内接する四角形の辺の長さ 面積を求める方法 数学i By Okボーイ マナペディア

三角比を用いた面積計算をマスターしよう スタディクラブ情報局

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

三角比と辺の長さの関係は 1分でわかる求め方 角度と辺の長さの比

高校数学 三角形の辺と角の関係 映像授業のtry It トライイット

簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく

余弦定理で角度を求める方法 数学の星

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

数i 基本的な三角比の値

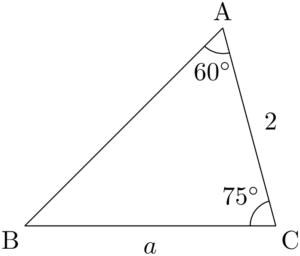
正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に

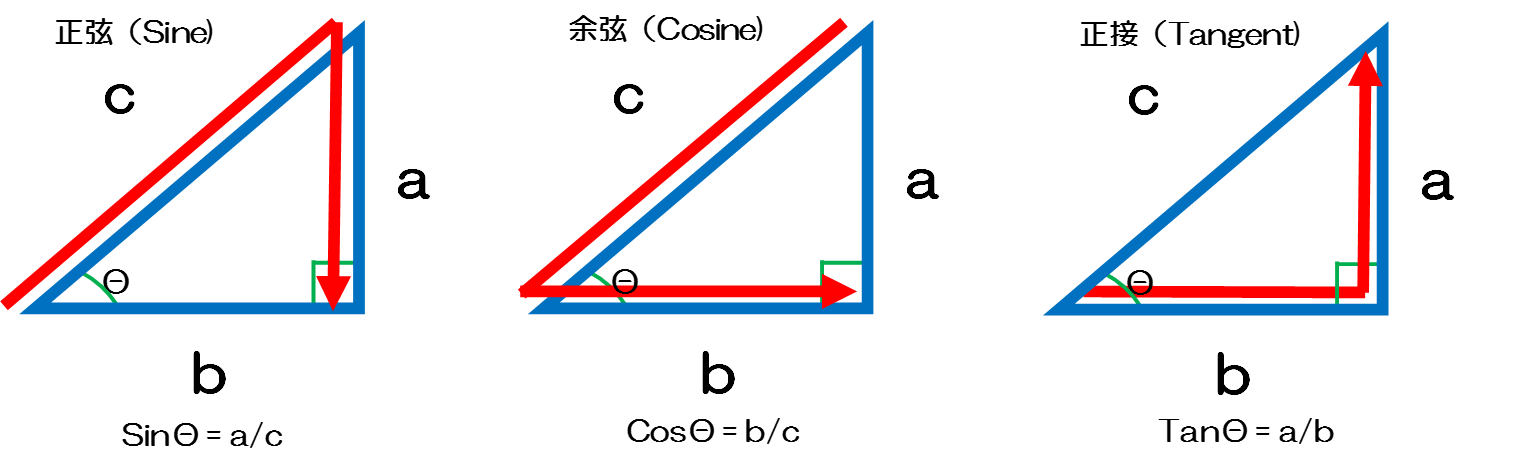
Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数

中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく

三角関数について

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

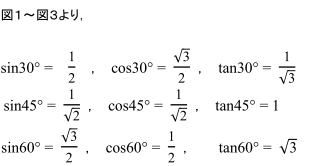
正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

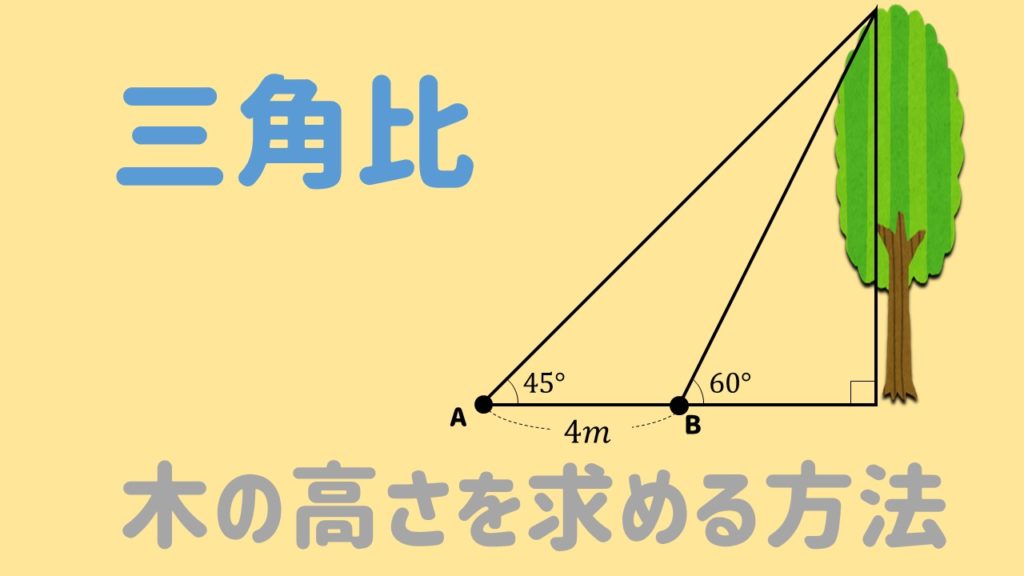
高1数学 木の高さを三角比を用いて求める方法を解説 数スタ

反射で求める三角比と辺の長さ 高校生 数学のノート Clear

高校数学 三角比を利用した長さの求め方1 例題編 映像授業のtry It トライイット

三角比から辺の長さを求める 数学i フリー教材開発コミュニティ Ftext

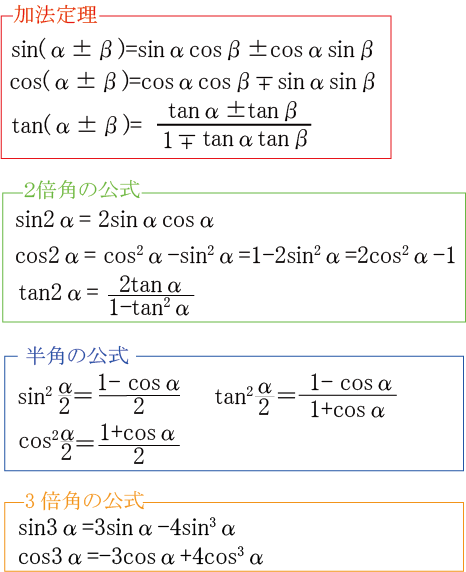
三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方

三角形の辺から角度を計算 製品設計知識

三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita

15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext

角度と底辺から斜辺と高さを計算 高精度計算サイト

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

三角関数のsin Cos Tanとは 図解ですぐわかる 超重要な公式と練習問題も 高校生向け受験応援メディア 受験のミカタ

15 シリーズの三角比 おいしい数学

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

高校数学 三角比を利用した長さの求め方2 例題編 映像授業のtry It トライイット

直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora

高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月

高校数学 三角比 辺の長さの求め方まとめと問題

タンジェントとは何か 中学生でも分かる三角関数の基礎

直角三角形の辺の長さ 合同条件 面積について アタリマエ

高校数学 三角比を利用した長さの求め方1 練習編 映像授業のtry It トライイット

わかりやすい三角比と基本公式 Irohabook

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

高校数学 三角比を利用した長さの求め方1 練習編 映像授業のtry It トライイット

数学ia 三角比の応用 大学入試数学の考え方と解法

三角比で辺の長さを表す問題がいまいちよく分かりません 求め方のポイントなど Yahoo 知恵袋

家電やスマホに必須 三角関数は陰の働き者 中高数学おさらい 三角関数 数列 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン

直角三角形の辺の長さ 合同条件 面積について アタリマエ

数学の勉強 三角比

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に

三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

Sin Cos 1 Cg Mathematics Ad04

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

日曜大工で使う数式

3

90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座

三角比と年周視差 星のこと

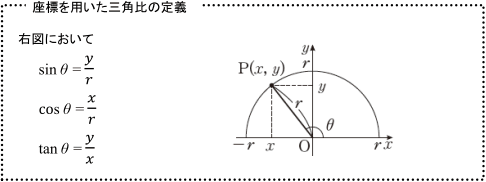
三角比の定義は １分でわかる定義 覚え方 表 直角三角形と単位円との関係

三角比の表の求め方について質問です 求め方を調べるとこんな感じに三 Yahoo 知恵袋

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

高校数学 三角比 辺の長さの求め方まとめと問題

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典

三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita

高校数学 三角比 辺の長さの求め方まとめと問題

直角 三角形 辺 の 長 さ 求め 方 直角三角形の解法 1 Documents Openideo Com

数i 基本的な三角比の値

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

三角関数の基礎知識

高校数学 三角比を利用した長さの求め方1 練習編 映像授業のtry It トライイット

三角比から辺の長さを求める 数学i フリー教材開発コミュニティ Ftext

高校1年三角比のところです 1 5を教えてください 求め方だけで結構です Clear

高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト

直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学

高1数学 木の高さを三角比を用いて求める方法を解説 数スタ

直角三角形の辺を求める Youtube

高校数学 数 ７６ 三角比 基本編 Youtube

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

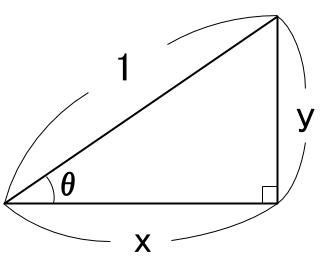
三角比の相互関係 高校数学の無料オンライン学習サイトko Su

高校数学 三角比を利用した長さの求め方2 例題編 映像授業のtry It トライイット

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

3

高校 数学 三角比６ 長さを求める１ 11分 Youtube